Définition
Soient \( E\subseteq \R^2\) , \( f:E\rightarrow\R\) une fonction à deux variables et \( (a, b)\in E\) .
- \( \bullet\)
- On dira que \( (a, b)\) est un maximum (resp. minimum) global si pour tout \( (x, y)\in E\) , \( f(x, y)\leqslant f(a, b)\) (resp. \( f(x, y)\geqslant f(a, b)\) ).
- \( \bullet\)
- On dira que \( (a, b)\) est un maximum (resp. minimum) global si pour tout \( (x, y)\in D\) , \( f(x, y)\leqslant f(a, b)\) (resp. \( f(x, y)\geqslant f(a, b)\) ).
Où \( D\subset E\) est un (petit) disque autour de \( (a, b)\) .
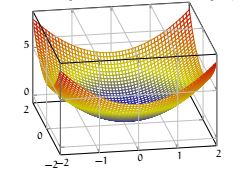
Par exemple, il est facile d'observer que \( (0, 0)\) est un minimum global de \( f(x, y)=x^2+y^2\) .
%
Définition
Soient \( E\subseteq \R^2\) , \( f:E\rightarrow\R\) une fonction à deux variables et \( (a, b)\in E\) .
On dira que \( (a, b)\) est un point critique si \( \overrightarrow{Grad}_{(a, b)}(f)=\overrightarrow{0}\) .
Reprenons l'exemple de la fonction \( f(x, y) = -x^2-xy+x+y^2\) et dont le gradient est \( \overrightarrow{Grad}_{(a, b)}(f)=\begin{pmatrix}
-2a-b+1\\
-a+2b
\end{pmatrix}
\) . Trouver les points critiques revient donc à résoudre le système
\[
\left\{
\begin{array}{rcl}
-2a-b+1=0\\
-a+2b=0
\end{array}
\right.
\]
Il est facile de voir que ce système admet une unique solution \( (a, b)=\left(\dfrac{1}{5}, \dfrac{2}{5}\right)\) . En conclusion, l'unique point critique de cette fonction est \( \left(\dfrac{1}{5}, \dfrac{2}{5}\right)\) .
Théorème [Fermat]
Soient \( E\subseteq \R^2\) , \( f:E\rightarrow\R\) une fonction à deux variables et \( (a, b)\in E\) .
Si \( (a, b)\) est un extrema local alors c'est un point critique.
Démonstration
Admise
En conclusion, pour déterminer un extremum, il suffit de déterminer les points critiques d'une fonction. Mais comment savoir si c'est un maximum ou un minimum. Réalisons quelques exemple à une variables.
Considérons la fonction \( f(x)=x^2\) . Sa dérivé est \( f'(x)=2x\) qui s'annule trivialement en \( x=0\) . Ainsi \( 0\) est un point critique. Nous savons, en regardant le graphique que c'est un minimum. Regardons la dérivé seconde : \( f''(x)=2\) ... c'est positif en \( x=0\) .
Considérons la fonction \( f(x)=-x^2\) . Sa dérivé est \( f'(x)=-2x\) qui s'annule trivialement en \( x=0\) . Ainsi \( 0\) est un point critique. Nous savons, en regardant le graphique que c'est un maximum. Regardons la dérivé seconde : \( f''(x)=-2\) ... c'est négatif en \( x=0\) .
Considérons la fonction \( f(x)=x^3\) . Sa dérivé est \( f'(x)=3x^2\) qui s'annule trivialement en \( x=0\) . Ainsi \( 0\) est un point critique. Regardons la dérivé seconde : \( f''(x)=6x\) ... nul en \( x=0\) .
Vous l'aurez compris, c'est en regardant du coté de la dérivé seconde que nous aurons une réponse.






