L'idée est d'imiter ce que nous savons faire avec les fonctions à une variable et d'obtenir un équivalent de l'outil qu'est la dérivée.
Sauf qu'il y a un problème avec la définition de dérivé. Avec une variable le nombre dérivé d'une fonction \( f\) en un point \( a\) est défini par la limite \( \lim{x\rightarrow a}\dfrac{f(x)-f(a)}{x-a}\) . Avec une variable, la notion de limite est assez claire, soit on se rapproche de \( a\) par la gauche, ce qui est noté \( \lim{x\rightarrow a^-}\) , soit par la droite, noté \( \lim{x\rightarrow a^+}\) . En effet, sur
une ligne, on peut moralement se rapprocher d'un nombre soit par la gauche soit par la droite.
Mais lorsque nous sommes avec deux variables, quel sens donner à la notion de limite ? Comment se rapprocher d'un point. Il y a plein de manière différente de se rapproche de \( (a, b)\) : en spirale, en ligne droite, de manière exponentielle ou logarithmique, comme une parabole etc... Est-ce qu'il existe une
meilleure manière de se rapprocher d'un point ou est-ce qu'il existe un
moyen universelle ?
La réponse à cette question est OUI. Mais dans le cadre de ce cours nous n'allons pas introduire cette notion qui nécessite de définir une distance et de parler de développement limité. Une autre manière d'introduire la dérivée avec plusieurs variables est de se servir des fonctions partielles et de les dériver.
Définition
Soient \( E\subseteq \R^2\) , \( f:E\rightarrow\R\) une fonction à deux variables et \( (a, b)\in E\) .
- \( \bullet\)
- La dérivé partielle de \( f\) par rapport à \( x\) en \( (a, b)\) est la dérivé de la fonction partielle \( f_{|y=b}(x)\) en \( x=a\) . On la note \( \dfrac{\partial f}{\partial x} (a, b)\) . Par définition c'est
\[\dfrac{\partial f}{\partial x} (a, b)=\lim{x\rightarrow a}\dfrac{f(x, b)-f(a, b)}{x-a}\]
- \( \bullet\)
- La dérivé partielle de \( f\) par rapport à \( y\) en \( (a, b)\) est la dérivé de la fonction partielle \( f_{|x=a}(y)\) en \( y=b\) . On la note \( \dfrac{\partial f}{\partial y} (a, b)\) . Par définition c'est
\[\dfrac{\partial f}{\partial y} (a, b)=\lim{y\rightarrow b}\dfrac{f(a, y)-f(a, b)}{y-b}\]
On définit, comme pour les fonction à une variables, les fonctions dérivées partielles en \( (a, b)\) .
En d'autres termes, la dérivée partielle \( \dfrac{\partial f}{\partial x}\) revient à "
oublier" que \( y\) est une variable dans l'expression de \( f(x, y)\) et de ne dériver qu'en considérant \( x\) comme variable et \( y\) comme constante.
En particulier, toutes les opérations classiques sur les dérivées s'appliquent.
Prenons par exemple la fonction \( f(x, y)=\dfrac{x}{x^2+y^2}\) définie sur \( \R^2-\{(0, 0)\}\) . Alors
En utilisant la dérivé de \( \dfrac{u}{v}\) qui est \( \dfrac{u'v-v'u}{v^2}\) :
\begin{eqnarray*}
\dfrac{\partial f}{\partial x}
&=&\dfrac{(1)\times (x^2+y^2)-(x)(2x)}{(x^2+y^2)}\\
&=&\dfrac{y^2-x^2}{(x^2+y^2)}
\end{eqnarray*}
En utilisant la dérivé de \( \dfrac{1}{u}\) qui est \( -\dfrac{u'}{u^2}\) , le \( x\) au numérateur étant considéré comme une constante :
\begin{eqnarray*}
\dfrac{\partial f}{\partial y}
&=&-\dfrac{x\times 2y}{(x^2+y^2)}\\
&=&-\dfrac{2xy}{(x^2+y^2)}
\end{eqnarray*}
Avec une seule variable le nombre dérivée représentait la vitesse, précisément le vecteur vitesse (c'est la tangente).
Avec deux variables, c'est la même chose. On parle du gradient.
Définition
Soient \( E\subseteq \R^2\) , \( f:E\rightarrow\R\) une fonction à deux variables et \( (a, b)\in E\) . Le gradient de \( f\) en \( (a, b)\) est le vecteur
\[\overrightarrow{Grad}_{(a, b)}(f)=\begin{pmatrix}
\dfrac{\partial f}{\partial x}(a, b)\\
\dfrac{\partial f}{\partial y}(a, b)
\end{pmatrix}
\]
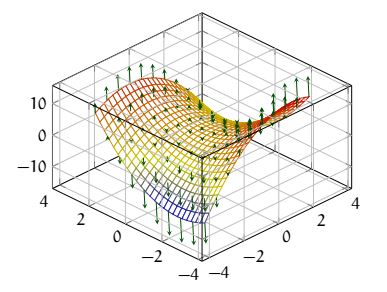
Considérons la fonction \( f(x, y) = -x^2-xy+x+y^2\) . Le gradient est \( \overrightarrow{Grad}_{(a, b)}(f)=\begin{pmatrix}
-2a-b+1\\
-a+2b
\end{pmatrix}
\) représenté en vert ci dessous.
%
Proposition
Le gradient d'une fonction en \( (a, b)\) est orthogonale à la ligne de niveau \( f(a, b)\) .
Démonstration
Admise
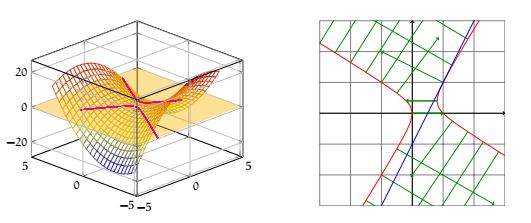
Reprenons la fonction précédente. Considérons le point \( (a, b)=(1, 1)\) . Le gradient est \( \overrightarrow{Grad}_{(1, 1)}(f)=\begin{pmatrix}
-2\\
1
\end{pmatrix}
\)
En dessin cela donne (en rouge la ligne de niveau \( f(1,1)=0\) ) en verts les gradients.
%
Corollaire
Soient \( E\subseteq \R^2\) , \( f:E\rightarrow\R\) une fonction à deux variables et \( (a, b)\in E\) tel que \( \overrightarrow{Grad}_{(a, b)}(f)\) existe et n'est pas le vecteur nul. Alors la droite tangente à la ligne de niveau \( f(a,b)\) a pour équation :
\[\dfrac{\partial f}{\partial x}(a, b)(x-a)+\dfrac{\partial f}{\partial y}(a, b)(y-b)=0\]
Démonstration
Soit \( A=(a, b)\) . Notons \( M=(x, y)\) un point de cette droite. Comme \( \overrightarrow{AM}\) est orthogonal à \( \overrightarrow{Grad}_{(a, b)}(f)\) (d'après la proposition précédente) on a \( \overrightarrow{Grad}_{(a, b)}(f)\cdot\overrightarrow{AM}=0\) ce qui traduit l'équation du corollaire.
Par exemple l'équation de la tangente en \( (1, 1)\) de la ligne de niveau \( 0\) de la fonction \( f(x, y) = -x^2-xy+x+y^2\) est \( -2(x-1)+1(y-1)=0\) soit la droite \( y=2x-1\) (en bleue sur le graphique précédent).
Que se passe-t-il si le gradient est nul ?







