Bien connue des élèves de terminales revenons de manière sibylline sur les fonctions à une variables
Voici la définition donnée par L. Euler.
Si certaines quantités dépendent d'autres quantités de telle manière que si les autres changent, ces quantités changent aussi, alors on a l'habitude de nommer ces quantités fonctions de ces dernières; cette dénomination a la plus grande étendue et contient en elle-même toutes les manières par lesquelles une quantité peut être déterminée par d'autre. Si, par conséquent, x désigne une quantité variable, alors toutes les autres quantités qui dépendent de x de n'importe quelle manière, ou qui sont déterminées par x, sont appelées fonctions de x.
Vocabulaire
- L'image
- d'un réel \( x\) par une fonction \( f\) est le réel \( f(x)\) . Avec la fonction \( f(x)=3x+4\) , au lieu de dire "la fonction \( f\) transforme le nombre réel \( -1\) en \( 1\) " on dira "l'image de \( -1\) par \( f\) est \( 1\) " ce qui est donc la même chose que d'écrire \( f(-1)=1\) .
- Un antécédent
- d'un réel \( y\) par une fonction \( f\) est un réel \( x\) tel que \( f(x)=y\) . Avec la fonction \( f(x)=3x+4\) , au lieu de dire "la fonction \( f\) transforme le nombre réel \( -1\) en \( 1\) " on dira "un antécédent \( 1\) par \( f\) est \( -1\) " ce qui est donc la même chose que d'écrire \( f(-1)=1\) .
- le domaine de définition
- est l'ensemble des valeurs possible pour la variable dans la définition de la fonction.
Si par exemple \( f(x)=\dfrac{\sqrt{x-10}}{x-20}\) alors il faut d'une part ne pas annuler le dénominateur, ce qui n'arrive que lorsque \( x=20\) et ne jamais avoir \( x-10 {{<}} 0\) ce qui arrive pour les réels de l'intervalle \( ]-\infty ; 10[\) . En définitive il faut enlever à \( \mathbb{R}\) ces impossibilités. On en conclut alors que le domaine de définition de cette fonction est \( [10; 20[\cup]20; +\infty[\) .
Attention ! On parle bien de LA image mais de UN antécédent. En effet, si on prend un nombre réel \( x\) dans le domaine de définition alors il a une et une seule image. Tandis que la recherche d'antécédent donne naissance à une équation qui peut avoir aucune, une, voir plusieurs solutions ! Par exemple, si \( g\) est une fonction définie par \( g(x)=x^2-3x\) et que nous cherchons les antécédents (éventuels) de \( -2\) alors nous sommes amené, par définition d'antécédent, à résoudre l'équation \( g(x)=-2\) soit encore \( x^2-3x=-2\) soit encore \( x^2-3x+2=0\) ce qui se résout à l'aide d'un discriminant et aboutis à \( 1\) et \( 2\) comme solution. D'ailleurs on vérifie sans peine que \( g(1)=1^2-3(1)=-2\) et que \( g(2)=2^2-3(2)=-2\) .
Représentation
Pour travailler avec les fonctions, il est d'accoutumer de les représenter dans un repère cartésien. Pour chaque valeur de \( x\) , dans le domaine de définition de la fonction, on marque, d'un point (ou d'une croix ou peu importe) le point du repère de coordonnée \( (x, f(x))\) et on relie les points consécutifs.
Reprenons l'exemple de la fonction \( f(x)=\dfrac{\sqrt{x-10}}{x-20}\) . On prend différente valeur et on place ces valeurs dans le repère :
\[
\begin{array}{r||c|c|c|c|c}
x&10&14&19&26&35\\\hline
f(x)&0&-\dfrac{1}{3}&-3&\dfrac{2}{3}&\dfrac{1}{3}
\end{array}
\]
Ce qui correspond aux points suivants :
Plus on va avoir de point, plus la fonction sera dessiner de manière précise.
Avec un peu plus de point on arrive à ce qui est appelé le
graphe de la fonction \( f\) ou
courbe représentative de la fonction \( f\) :
Limites
Si une fonction n'a pas de valeurs interdites alors elle n'a pas de problème pour le calcul de ses limites. La notion qui est caché derrière ce
bon comportement des fonctions est la notion de continuité.
Théorème
Soit \( f\) une fonction définie (et continue) en \( a\in \mathbb{R}\) dans le domaine de définition de la fonction, alors
\[\underset{x\rightarrow a}{lim} \ f(x)=f(a)\]
Les cas problématiques viennent en générale des infinis.
Théorème
\[
\underset{x\rightarrow 0^+}{lim} \ \dfrac{1}{x}=+\infty\qquad
\underset{x\rightarrow 0^-}{lim} \ \dfrac{1}{x}=-\infty
\]
\[
\underset{x\rightarrow +\infty}{lim} \ \dfrac{1}{x}=0\qquad
\underset{x\rightarrow -\infty}{lim} \ \dfrac{1}{x}=0
\]
- Inversion de limites.
- Inverser une limite est relativement facile si on garde en tête que l'inverse de 0 c'est de l'infini et que l'inverse de l'infini c'est 0.
\[
\begin{array}{|c|c|c|}
\hline
\lim{x\rightarrow a}f(x)&\lim{x\rightarrow a}\dpl{\frac{1}{f(x)}}\\\hline\hline
l\neq 0 & \dpl{\frac{1}{l}}\\\hline
0^+& +\infty\\\hline
0^-& -\infty\\\hline
\pm\infty & 0\\\hline
\end{array}
\]
- Somme de limite.
-
\[
\begin{array}{|c|c|c|}
\hline
\lim{x\rightarrow a}f(x)&\lim{x\rightarrow a}g(x)&\lim{x\rightarrow a}f(x)+g(x)\\\hline\hline
l&l'&l+l'\\\hline
l&\pm\infty&\pm\infty\\\hline
+\infty&+\infty&+\infty\\\hline
-\infty&-\infty&-\infty\\\hline
+\infty&-\infty&\text{F.I.}\\\hline
\end{array}
\]
- Produit d'une limite par un nombre.
-
\[
\begin{array}{|c|c|c|}
\hline
\lim{x\rightarrow a}f(x)&\lim{x\rightarrow a}\lambda f(x)\\\hline\hline
l&\lambda l\\\hline
+\infty&+\infty \text{ si }\lambda{>}0\\\hline
+\infty&-\infty \text{ si }\lambda{<}0\\\hline
-\infty&-\infty \text{ si }\lambda{>}0\\\hline
-\infty&+\infty \text{ si }\lambda{<}0\\\hline
\end{array}
\]
- Produit de deux limites.
-
\[
\begin{array}{|c|c|c|}
\hline
\lim{x\rightarrow a}f(x)&\lim{x\rightarrow a}g(x)&\lim{x\rightarrow a}f(x)\times g(x)\\\hline\hline
l&l'&l\times l'\\\hline
+\infty&+\infty&+\infty\\\hline
-\infty&-\infty&+\infty\\\hline
+\infty&-\infty&-\infty\\\hline
l{>}0&+\infty&+\infty\\\hline
l{<}0&+\infty&-\infty\\\hline
l{>}0&-\infty&-\infty\\\hline
l{<}0&-\infty&+\infty\\\hline
0&\pm\infty&F.I.\\\hline
\end{array}
\]
- Quotient de deux limites.
- Un quotient n'est rien d'autre qu'un produit avec un inverse : \( \dfrac{f(x)}{g(x)}=f(x)\dfrac{1}{g(x)}\) .
Retenez les 4 formes indéterminées :
\[\infty-\infty\qquad 0\times \infty\qquad \dfrac{0}{0} \qquad \dfrac{\infty}{\infty}\]
Dérivation
Définition
Soit \( f\) une fonction définie en \( a\in \mathbb{R}\) de son domaine de définition. Si
\[\lim{x\rightarrow a^+}\dfrac{f(x)-f(a)}{x-a}=
\lim{x\rightarrow a^-}\dfrac{f(x)-f(a)}{x-a}
\]
et que ces deux limites sont finies, alors on appellera la valeur de ces limites la dérivé de la fonction \( f\) en \( a\) que l'on notera \( f'(a)\) . Précisément :
\[
f'(a)=\lim{x\rightarrow a}\dfrac{f(x)-f(a)}{x-a}
\]
Quelque soit la fonction que nous traitons, cette limite est toujours une forme indéterminée (de la forme \( 0/0\) ). Ca serait beaucoup moins intéressant sinon
^_^.
Par exemple dérivons en \( a=3\) la fonction \( f(x)=x^2\) . Revenons à la définition et essayons de simplifier la limite, qui est malheureusement par construction, toujours une forme indéterminée. Ici l'idée est d'utiliser une identité remarquable.
\begin{eqnarray*}
f'(3)&=&\lim{x\rightarrow 3} \dfrac{x^2-3^2}{x-3}\\
&=& \lim{x\rightarrow 3} \dfrac{(x-3)(x+3)}{x-3}\\
&=& \lim{x\rightarrow 3}(x+3)\\
&=& 6
\end{eqnarray*}
Conclusion \( f'(3)=6\) .
Nous venons de voir la définition qui en tant que tel n'est pas évidente de prime abord. Et nous espérons que vous l'aurez compris, ça sert à calculer la vitesse instantanée. Mais tout ce travail pour calculer une vitesse serait un peu trop de gâchis de concept mathématiques. Puis surtout, en pratique comme procède t-on au calcul ? Les réponses arrivent !
Tangente
Définition
L'équation de la tangente à la courbe représentative d'une fonction \( f\) définie en un réel \( a\) est donnée par
\[
T_a\quad : \quad Y=f'(a)(X-a)+f(a)
\]
Par exemple la tangente de la fonction carré en \( a=3\) est \( T_3:\ y=6(x-3)+3^2=6x-9\)
Dérivées usuelles et fonctions dérivées
Dans le calcul que nous avions fait dans les paragraphes précédents pour calculer la dérivée de la fonction carré en \( 3\) , que l'on ai mis un \( 3\) ou un \( 42\) ça ne change pas le travail :
\begin{eqnarray*}
f'(a)&=&\lim{x\rightarrow a} \dfrac{x^2-a^2}{x-a}\\
&=& \lim{x\rightarrow a} \dfrac{(x-a)(x+a)}{x-a}\\
&=& \lim{x\rightarrow a}(x+a)\\
&=& 2a
\end{eqnarray*}
Le cas de la fonction carré est réglé ! C'est l'occasion de parler de
fonction dérivée.
Définition
La fonction dérivée d'une fonction \( f\) est la fonction notée \( f'\) tel que la valeur de \( f'\) en \( a\) est le nombre dérivé de la fonction \( f\) en \( a\) .
Nous avons par exemple montré que la fonction dérivée de la fonction carré est \( f'(x)=2x\) .
Qu'en est-il de la fonction cube \( g(x)=x^3\) . Abracadabra ! Voici une formule sorti de nul part : \( x^3-y^3=(x-y)(x^2+xy+y^2)\) . Attaquons à présent le calcul de la limite :
\begin{eqnarray*}
g'(a)&=&\lim{x\rightarrow a} \dfrac{x^3-a^3}{x-a}\\
&=& \lim{x\rightarrow a} \dfrac{(x-a)(x^2+ax+a^2)}{x-a}\\
&=& \lim{x\rightarrow a} (x^2+ax+a^2)\\
&=& 3a^2
\end{eqnarray*}
En conclusion \( g'(x)=3x^2\) .
Commençons par faire peur : OUI ! Pour calculer des dérivées (en tant que fonction ou valeur numérique) il n'y a pas d'autre solution que de passer par la définition de limite ! Mais pas d'inquiétude. Beaucoup de mathématiciens ont établis un formulaire recensant les dérivées des fonctions usuelles (et oui, il faut les apprendre et les connaitre par cœur) :
Proposition
Soit \( n\) un entier strictement positif et \( k\) un nombre réel alors
\[f(x)=k\qquad \Rightarrow \qquad f'(x)=0\]
\[f(x)=x^n\qquad \Rightarrow \qquad f'(x)=nx^{n-1}\]
\[f(x)=\dfrac{1}{x^n}\qquad \Rightarrow \qquad f'(x)=-\dfrac{n}{x^{n+1}}\]
\[f(x)=\sqrt{x}\qquad \Rightarrow \qquad f'(x)=\dfrac{1}{2\sqrt{x}}\]
On retrouve par exemple les formules que nous avons trouvé à l'aide du calcul de limite sur les fonctions carré et cube.
Opérations sur les dérivées
Et si nous souhaitions dériver la fonction \( x+1\) ? Nous savons dérivé \( x=x^1\) qui admet \( 1x^0=1\) comme dérivé et la dérivé du nombre réel \( 1\) est \( 0\) . Qu'en est-il de la somme ?
Proposition
\[(f+g)'=f'+g'\]
Démonstration
En passant à la limite dans cette formule on prouve le résultat.
\[\dfrac{[f(x)+g(x)]-[f(a)+g(a)]}{x-a}=\dfrac{f(x)-f(a)}{x-a}+\dfrac{f(x)-f(a)}{x-a}\]
Ainsi la fonction dérivée de \( x^2+x+1\) est \( 2x+1\) .
Qu'en est-il de la fonction dérivée de la \( x^2-3x+\dfrac{1}{x}\) . Les précédents résultats nous donnent \[\left(x^2-3x+\dfrac{1}{x}\right)'=
\left(x^2\right)'-\left(3x\right)'+\left(\dfrac{1}{x}\right)'=
2x-\left(3x\right)'-\dfrac{1}{x^2}
\]
Réglons le problème de \( \left(3x\right)'\) à coup de théorème !
Proposition
\[(\lambda f)'=\lambda f'\]
Démonstration
En passant à la limite dans cette formule on prouve le résultat.
\[
\dfrac{\lambda f(x)-\lambda f(a)}{x-a}=\lambda\dfrac{f(x)-f(a)}{x-a}
\]
En d'autre terme la dérivé de \( 3x\) c'est \( 3\) fois la dérivée de \( x\) (qui est \( 1\) ). Au final
\[\left(x^2-3x+\dfrac{1}{x}\right)'=
2x-3-\dfrac{1}{x^2}
\]
Et qu'en est-il de la fonction dérivée de \( (\sqrt{x}+1)\times \dfrac{1}{x}\) . Bon soyons claire : ca va commencer a devenir n'importe quoi, mais ça marche !
Proposition
\[(fg)'=f'g+g'f\]
Démonstration
En passant à la limite dans cette égalité on prouve le résultat :
\begin{eqnarray*}
\dfrac{f(x)g(x)-f(a)g(a)}{x-a}&=&\dfrac{f(x)g(x)-f(x)g(a)+f(x)g(a)-f(a)g(a)}{x-a}\\
&=&\dfrac{f(x)g(x)-f(x)g(a)}{x-a}+\dfrac{f(x)g(a)-f(a)g(a)}{x-a}\\
&=&f(x)\dfrac{g(x)-g(a)}{x-a}+g(a)\dfrac{f(x)-f(a)}{x-a}
\end{eqnarray*}
Ainsi
\begin{eqnarray*}
\left((\sqrt{x}+1)\dfrac{1}{x}\right)'&=&
(\sqrt{x}+1)'\dfrac{1}{x}+(\sqrt{x}+1)\left(\dfrac{1}{x}\right)'\\
&=&\dfrac{1}{2\sqrt{x}}\dfrac{1}{x}+(\sqrt{x}+1)\left(-\dfrac{1}{x^2}\right)
\end{eqnarray*}
En conclusion \( \left((\sqrt{x}+1)\dfrac{1}{x}\right)'=\dfrac{1}{2x\sqrt{x}}-\dfrac{\sqrt{x}+1}{x^2}\) (les plus savant pour chercher à simplifier davantage cette dérivée et montrer que \( \left((\sqrt{x}+1)\dfrac{1}{x}\right)'=-\dfrac{\sqrt{x}+2}{2x^2}\) en utilisant le fait que \( \sqrt{x}^2=x\) ).
Et qu'en est-il de la fonction dérivée de la fonction \( \dfrac{x}{x+1}\) ?
Proposition
\[\left(\dfrac{f}{g}\right)'=\dfrac{f'g-g'f}{g^2}\]
Démonstration
En passant à la limite dans cette égalité on prouve le résultat :
\begin{eqnarray*}
\dfrac{\dfrac{f(x)}{g(x)}-\dfrac{f(a)}{g(a)}}{x-a}&=&
\dfrac{\dfrac{f(x)g(a)}{g(x)g(a)}-\dfrac{g(x)f(a)}{g(x)g(a)}}{x-a}\\
&=&
\dfrac{\dfrac{f(x)g(a)-g(x)f(a)}{g(x)g(a)}}{x-a}\\
&=&
\dfrac{f(x)g(a)-g(x)f(a)}{g(x)g(a)(x-a)}\\
&=&
\dfrac{f(x)g(a)-f(a)g(a)+f(a)g(a)-g(x)f(a)}{g(x)g(a)(x-a)}\\
&=&
\dfrac{f(x)g(a)-f(a)g(a)}{g(x)g(a)(x-a)}+\dfrac{f(a)g(a)-g(x)f(a)}{g(x)g(a)(x-a)}\\
&=&
\dfrac{f(x)g(a)-f(a)g(a)}{g(x)g(a)(x-a)}-\dfrac{f(a)g(x)-g(a)f(a)}{g(x)g(a)(x-a)}\\
&=&
g(a)\dfrac{f(x)-f(a)}{g(x)g(a)(x-a)}-f(a)\dfrac{g(x)-g(a)}{g(x)g(a)(x-a)}\\
&=&\dfrac{g(a)\dfrac{f(x)-f(a)}{x-a}-f(a)\dfrac{g(x)-g(a)}{x-a}}{g(x)g(a)}
\end{eqnarray*}
Sur notre exemple
\begin{eqnarray*}
\left(\dfrac{x}{x+1}\right)'&=&
\dfrac{(x)'(x+1)-(x+1)'(x)}{(x+1)^2}\\
&=&\dfrac{1(x+1)-1(x)}{(x+1)^2}\\
&=&\dfrac{1}{(x+1)^2}
\end{eqnarray*}
Et qu'en est-il de la fonction dérivé de \( \sqrt{x^2+x}\) ?
Proposition
\[(f(g))'=f'(g)\times g'\]
Démonstration
On a
\[\dfrac{f(g(x))-f(g(a))}{x-a}=\dfrac{f(g(x))-f(g(a))}{g(x)-g(a)}\times \dfrac{g(x)-g(a)}{x-a}\]
D'un coté \( \lim{x\rightarrow a} \dfrac{g(x)-g(a)}{x-a}=g'(a)\) de l'autre coté en effectuant le changement de variable \( y=g(x)\) on a, par définition du nombre dérivée \( \lim{x\rightarrow a} \dfrac{f(g(x))-f(g(a))}{g(x)-g(a)}=\lim{y\rightarrow g(a)} \dfrac{f(y)-f(g(a))}{y-g(a)}=f'(g(a))\) .
Ainsi \( (\sqrt{x^2+x})'=\dfrac{1}{2\sqrt{x^2+x}}\times (x^2+x)'=\dfrac{1}{2\sqrt{x^2+x}}\times (2x+1)=
\dfrac{2x+1}{2\sqrt{x^2+x}}\)
En particulier ce dernier résultat permet d'obtenir un petit peu plus de formule de dérivation (il n'y en avait pas assez comme ça !)
Corollaire
Soient \( n\) un entier strictement positif \( u\) une fonction
\[f(x)=u(x)^n\qquad \Rightarrow \qquad f'(x)=nu(x)^{n-1}\times u'(x)\]
\[f(x)=\dfrac{1}{u(x)^n}\qquad \Rightarrow \qquad f'(x)=-\dfrac{n}{u(x)^{n+1}}\times u'(x)\]
\[f(x)=\sqrt{u(x)}\qquad \Rightarrow \qquad f'(x)=\dfrac{1}{2\sqrt{u(x)}}\times u'(x)\]
Par exemple déterminons l'équation de la tangente à la courbe représentative de la fonction \( f\) définie sur \( \mathbb{R}\) par \( f(x)=\dfrac{1}{2}x^2-x+1\) en \( a=0\) .
D'après les paragraphes précédents \( T_0:\ y=f'(0)(x-0)+f(0)\) . D'une part \( f'(x)=x-1\) d'où \( f'(0)=-1\) et d'autre part \( f(0)=1\) . En conclusion l'équation de la tangente est \( y=-x+1\) .
Variations et dérivations
Lorsque l'on se donne une fonction, on souhaite l'étudier. Ce que nous avons déja explorer avec l'étude du domaine de définition ou des translations de fonction de références. D'autre informations son a extraire de la fonction. L'une d'elle est ce que l'on appelle les
variations de la fonction ce qui se traduit vulgairement par : quand est-ce que la fonction monte et quand-est-ce qu'elle descend.
Définition
- \( \bullet\)
- On dira qu'une fonction \( f\) est strictement croissante sur un intervalle \( I\) si pour tout réels \( \alpha\) et \( \beta\) de \( I\) tel que \( \alpha {<} \beta\) alors \( f(\alpha){<}f(\beta)\) .
- \( \bullet\)
- On dira qu'une fonction \( f\) est croissante sur un intervalle \( I\) si pour tout réels \( \alpha\) et \( \beta\) de \( I\) tel que \( \alpha {<} \beta\) alors \( f(\alpha)\leqslant f(\beta)\) .
- \( \bullet\)
- On dira qu'une fonction \( f\) est strictement décroissante sur un intervalle \( I\) si pour tout réels \( \alpha\) et \( \beta\) de \( I\) tel que \( \alpha {<} \beta\) alors \( f(\alpha){>}f(\beta)\) .
- \( \bullet\)
- On dira qu'une fonction \( f\) est décroissante sur un intervalle \( I\) si pour tout réels \( \alpha\) et \( \beta\) de \( I\) tel que \( \alpha {<} \beta\) alors \( f(\alpha)\geqslant f(\beta)\) .
Plaçons nous par exemple sur l'intervalle \( ]0 ; +\infty[\) et étudions les variations de la fonction \( f(x)=x^2\) . Soit \( 0{<}\alpha{<}\beta\) alors
\[f(\alpha)-f(\beta)=\alpha^2-\beta^2=(\alpha-\beta)(\alpha+\beta)\]
Puisque \( \alpha\) et \( \beta\) sont tout deux positifs alors \( \alpha+\beta{>}0\) et puisque \( \alpha {<} \beta\)
alors \( \alpha-\beta{<}0\) . La règle des signes nous donne donc que \( \alpha^2-\beta^2\) est négatif soit encore \( f(\alpha){<}f(\beta)\) et donc que la fonction carré est strictement croissante sur \( ]0; +\infty[\)
On montrerai de même que la fonction carré est strictement décroissante sur \( ]-\infty; 0[\) .
Pour compiler ces informations de variation on réalise un
tableau de variation qui comporte deux lignes : une ligne pour spécifier les valeurs de \( x\) classer dans l'ordre croissant, comme pour les tableaux de signe et une seconde ligne représentant les variations par des flèches qui montent pour signaler la croissance ou qui descende pour signaler la décroissance.
Le tableau de variation de la fonction carré est donc le suivant :
On complète souvent le tableau de variation en mettant les valeurs des limites au bout des flèches :
Cet exemple était assez facile. Les droites, c'est à dire les fonctions affines ont aussi des variations faciles à étudier.
Proposition
Soit \( f\) une fonction affine de coefficient directeur \( a\) .
- \( \bullet\)
- Si \( a{>}0\) la droite est strictement croissante.
- \( \bullet\)
- Si \( a{<}0\) la droite est strictement décroissante.
- \( \bullet\)
- Si \( a=0\) la droite est constante.
où \( f(x)=k\)
Théorème
- \( \bullet\)
- Si \( f'\) existe et est positive sur un intervalle \( I\) alors la fonction \( f\) est croissante sur \( I\) .
- \( \bullet\)
- Si \( f'\) existe et est négative sur un intervalle \( I\) alors la fonction \( f\) est décroissante sur \( I\) .
Autrement dis : étudier les variations d'une fonction reviens à étudier le signe de sa dérivé.
La dérivé de la fonction \( f(x)=x^2\) est \( f'(x)=2x\) . Naturellement \( 2x\) est positif lorsque \( x\) est positif donc la fonction \( f\) sera croissante sur cet intervalle ce que nous avions déjà déterminer.
Exemple
Étudions la fonction \( f(x)=x+\dfrac{x}{x^2-1}\) .
Nous voyons une fraction, il faut donc que le dénominateur, \( x^2-1\) , ne s'annule pas. En utilisant une identité remarquable ou une les formules de calculs des racines pour les polynômes de degrés 2, nous pouvons rapidement conclure que le domaine de définition de cette fonction est \( \mathbb{R}-\{-1 ; 1\}\) . Le but étant de déterminer le signe de la dérivé, c'est à dire de résoudre une inéquation de la forme \( f'(x){>}0\) , nous allons calculer la dérivée et la factoriser au maximum.
\begin{eqnarray*}
f'(x)&=&
1+\dfrac{(x)'(x^2-1)-(x^2-1)x}{(x^2-1)^2}\\
&=&
\dfrac{(x^2-1)^2+1(x^2-1)-2xx}{(x^2-1)^2}\\
&=&
\dfrac{(x^2-1)^2+x^2-1-2x^2}{(x^2-1)^2}\\
&=&
\dfrac{x^4-2x^2+1+x^2-1-2x^2}{(x^2-1)^2}\\
&=&
\dfrac{x^4-3x^2}{(x^2-1)^2}\\
&=&
\dfrac{x^2(x^2-3)}{(x^2-1)^2}
\end{eqnarray*}
Nous allons a présent dresser le tableau de signe et
par la même le tableau de variation.
La forme est donc la suivante.
%

Dans le tableau de variation comme dans les tableaux de signe on signale les valeurs interdites par une double barre.
%
En complétant les signes on arrive à
%
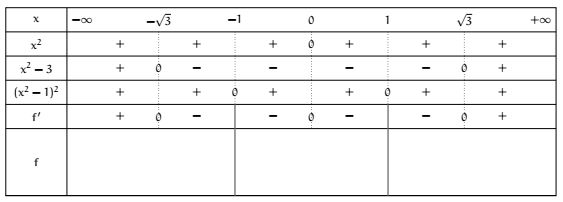
D'après le cours, une dérivée positive donner une fonction croissante et inversement, ce qui permet d'arriver aux variations suivantes :
%
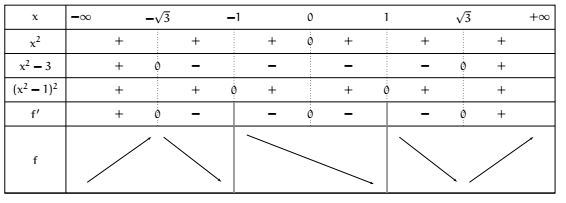
Une étude de limite permet alors de finaliser le tableau :
%
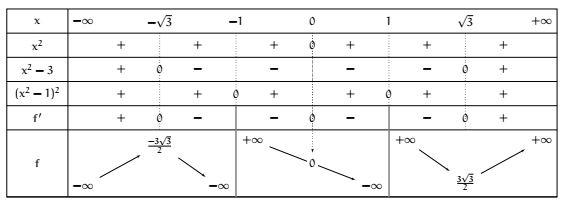
Le tableau de variation suffit en générale pour donner l'allure de la courbe représentative de la fonction \( f\) .
D'une part les valeurs finie de la fonction donne des point de passage. Dans notre exemple nous savons que la courbe passera par les points \( \left(-\sqrt{3}, -\dfrac{3\sqrt{3}}{2}\right)\) , \( \left(0, 0\right)\) et \( \left(\sqrt{3}, \dfrac{3\sqrt{3}}{2}\right)\) .
De plus, par construction, le coefficient directeur d'une tangente est le nombre dérivé. Lorsque la dérivée s'annule, on en déduit que la tangente est horizontale. Cela donnera une information sur le comportement autour de la tangente puisque par définition de
tangente, cette droite "frôle" la courbe. Ainsi la courbe sera horizontale autour des tangente horizontale !
On trace donc des morceaux de droite horizontale lorsque la dérivée s'annule :
Pour obtenir finalement











